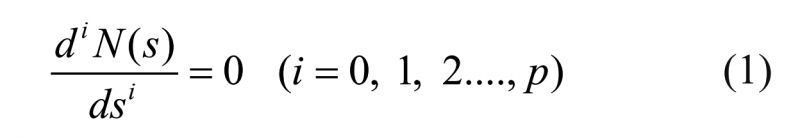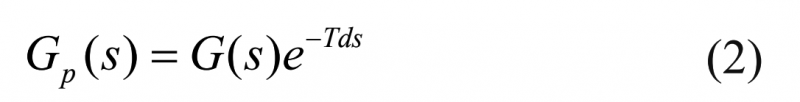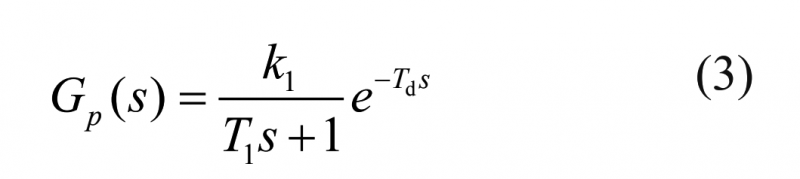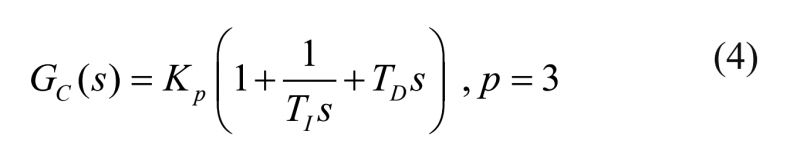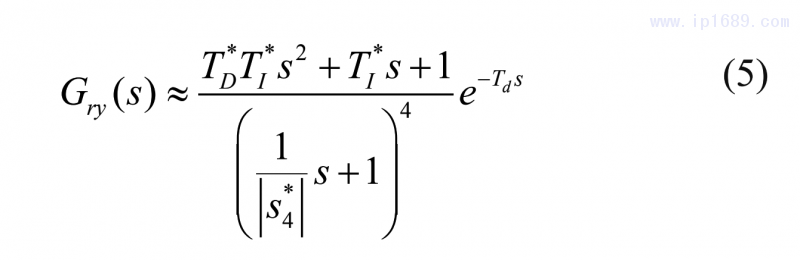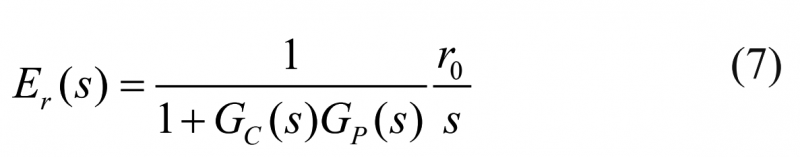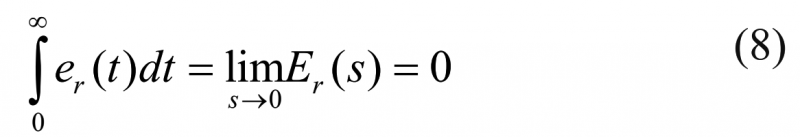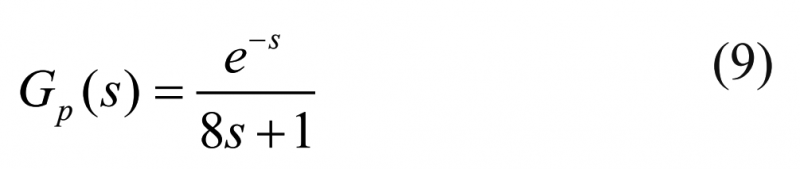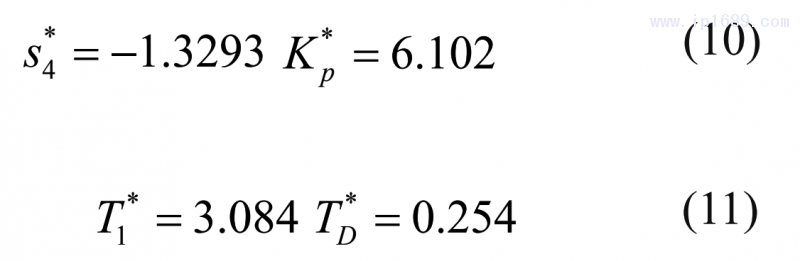您當前的位置：首頁 >> 技術 >> 吹塑 » 正文

基于MDP方法設計的PID控制器在吹塑機中的應用

瀏覽次數：5282 發布時間：2020年09月07日 08:54:18

[導讀] 塑料薄膜制造中吹塑機的張力控制是決定塑料薄膜厚度、強度和質量的一個重要因素。針對吹塑機的張力控制系統的一階積分時滯模型，提出一種新的基于MDP方法的PID控制器。

王軍峰1，徐越群1，蔡承才2

1.石家莊鐵路職業技術學院，河北石家莊 050061；2.石家莊鐵道大學，河北石家莊 050043

摘要：塑料薄膜制造中吹塑機的張力控制是決定塑料薄膜厚度、強度和質量的一個重要因素。針對吹塑機的張力控制系統的一階積分時滯模型，提出一種新的基于MDP方法的PID控制器。基于一個假設，即多主導極是正的、穩定的，并且過程控制系統無振蕩，同時需要假設非主導的極點或者零點對控制過程的影響不顯著。為了提高伺服性能，降低超調量，在PID控制結構中使用了設定點權重參數。控制過程簡潔，控制器參數以表達式的形式給出。仿真案例實驗結果表明，設計具有良好的追蹤性能和調節性能，并且魯棒性良好，適用于張力控制。

關鍵詞：吹塑機；張力控制；PID控制器；MDP；設定點權重參數

塑料薄膜在我國的產量約占全部塑料制品產量的20%，同時塑料薄膜的生產量增漲速度在所有塑料制品中最快[1]，各行各業對塑料薄膜的需求量也在逐年增長[2]。塑料薄膜應用范圍十分廣泛，涉及農業[3]、工業[4]、商業以及人們日常生活中的方方面面[5]。

塑料薄膜在制造過程中，首先需要把塑料材料加熱熔融，使用各種方法將其塑造成膜狀[6]。這些方法包括壓延法[7]、拉伸法[8]和吹塑法[9]。其中吹塑法需要將塑料熔融材料進行縱向和橫向的雙向拉伸，因此制造出的塑料薄膜強度較好，是應用最廣泛的塑料薄膜成型方法[10-11]。

在吹塑機的工作過程中，最關鍵的技術就是其張力控制系統的控制[12]，它決定了塑料薄膜產品的厚度、均勻程度、強度和品質[13]。目前，國內的大中型塑料薄膜生產制造商使用的吹塑機大多依賴進口[14]。因此針對塑料薄膜制造研究吹塑機的張力控制意義重大。

目前工業中大多采用PID控制結構，吹塑機的張力控制也是如此[15]。PID控制器不僅能夠通過合理設計提高張力控制精度，其較強的擾動抑制性也能使得吹塑機在電磁擾動等各種擾動情況下依舊維持穩定運行[16]。目前，各種文獻中記載了很多種關于設計PID控制器的方法，如直接綜合法[17]、Z-N法[18]、頻域法[19]、實證法[20]、內模控制法[21]、等值系數法[22]、二自由度控制法[23-24]、穩定分析法[25]和各種最優化算法[26-27]等。這些方法具有一定的優點，比如直接綜合法設計過程簡單明了、計算量少，但是對于擾動性能的提高有一定局限性[28]；Z-N法是最經典的方法，操作簡單，但是性能較差[29]；內模控制法雖然性能優良，但是計算過程較為繁復，使用條件較為苛刻，普適性較差；最優算法編程復雜，且存在大量迭代和模擬驗證過程。

本研究針對塑料薄膜生產中的吹塑機的張力控制系統，提出一種新的基于MDP(Multiple Dominant Pole-placement)的PID控制器的設計方法。這種方法基于一個假設，即存在多主導極點，并且其是正的、穩定的，過程控制無振蕩。同時，需要假設非主導的極點或者零點對控制過程的影響不顯著。這種方法過程簡潔，控制器參數將以表達式的形式給出，控制效果良好，適用于張力控制系統的設計。

01 方法設計

1.1 PID控制結構的設計

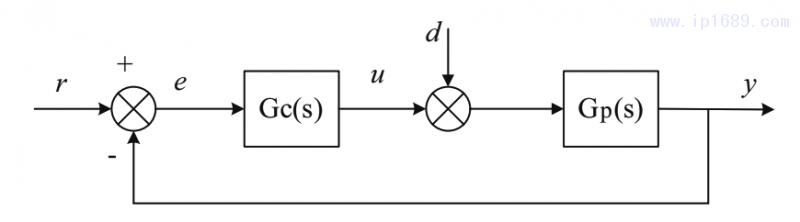
圖1為所設計的PID控制結構。

圖1中，r為期望變量；e為控制誤差；u為操縱變量；d為擾動量；y為被控變量；Gc(s)為PID控制器；Gp(s)為過程系統模型。

多主導極點S*p + 1 可以通過式(1)得到：

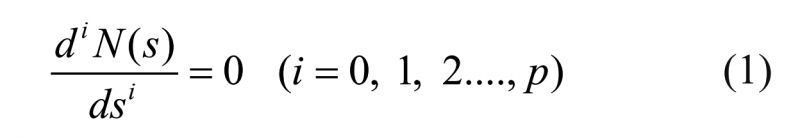
式（1）中：N(s)為針對有時滯的或者沒有時滯的過程系統與PID控制器組成的閉環控制系統特征擬多項式；p為控制器的可調整參數的數量。

圖1中的過程系統模型Gp(s) 將由式（2）表示：

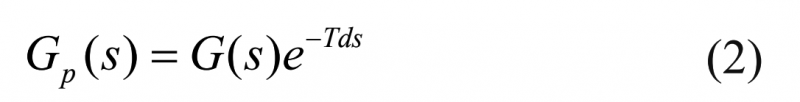
吹塑機的張力控制系統屬于一階積分系統，將式（2）細化為式（3）：

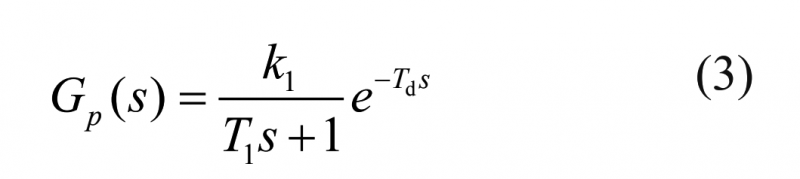
PID控制器的傳遞函數為：

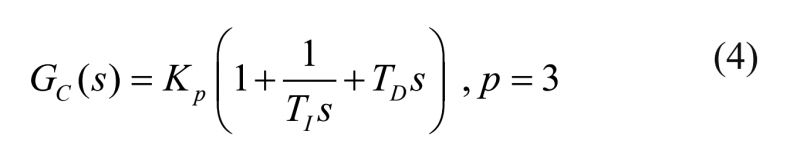
式中：G (s)為過程傳遞函數去掉時滯的部分；kc為控制器增益；TI為積分時間；TD為微分時間；Kp為控制器增益；Td為過程滯后時間。

1.2 基于MDP方法的PID控制算法

根據系統方程(1)的過程系統方程(2)和標準PID控制器(4),可以得到四重主導極點S*4和3個可調整參數K*P，T*I，T*D，過程系統(2)的近似系統傳遞函數和標準PID控制器(4)將通過MDP方法調整為:

式(5)中的擬多項式是Hurwitz多項式，它的零點加速了瞬態過程并且產生了伺服響應中不被許可的過大超調量，對于標準的PID控制器，假設式(5)的相等關系恒定，當出現下面不平等關系時，超調量將出現：

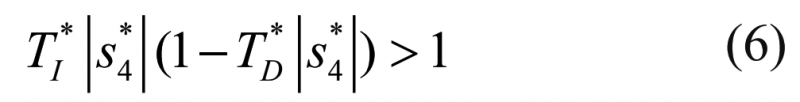
對于積分系統式(6)的不平等關系將一直成立，因此伺服響應中的超調量不能被移除。事實上，標準的PID控制器在控制積分系統時，不能實現沒有超調量的伺服響應也許能以另一種方式實現。

標準PID控制器和積分過程系統組成的閉環系統的控制誤差，在期望輸入變量 r(t) =r0的作用下將表示為：

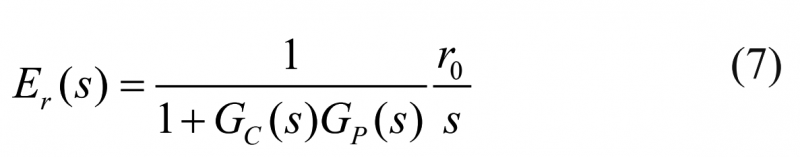
因為在控制區域它將成立以下關系：

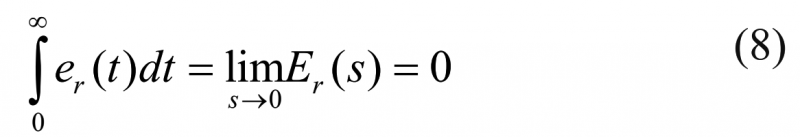
顯然，伺服響應無法實現無超調量。對式（8）解釋如下：伺服響應超過和低于r(t) =r0的中線區域是相等的。這個結論不僅對于MDP方法設計的控制系統，還廣泛適用于所有的積分系統。因此考慮在輸入信號后面加入設定點權重參數，以減小超調量并加快響應速度。

Arbogast等[30]和Begum等[31]使用了設定點權重參數，這樣使得閉環傳遞函數零點從虛軸移除并且減少了超調量和穩定時間。ε作為設定點權重參數，在選擇它時要求閉環系統響應沒有超調和設置時間并且響應曲線是平滑的。因此ε應該設定在0~1這個范圍之內。一般來說ε值大(接近于1)，在設定點響應的時候會產生很大的超調量，而ε值小的時候，系統響應會變慢。Begum等[31]中經過大量的仿真研究提出，常規設定點權重參數ε=0.4時效果最佳。區別于常規PID，本研究將設定點權重參數設為ε=0.5以提高追蹤性能。

表1為通過MDP方法計算得到的PID的可調整參數。表1為通過MDP方法計算得到的PID的可調整參數。

02 實例仿真

進行了一個由吹塑機張力控制系統一階積分時滯系統模型來進行PID控制器的設計：

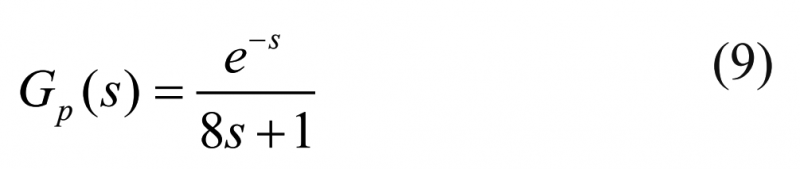
據MDP方法計算得到的參數為：
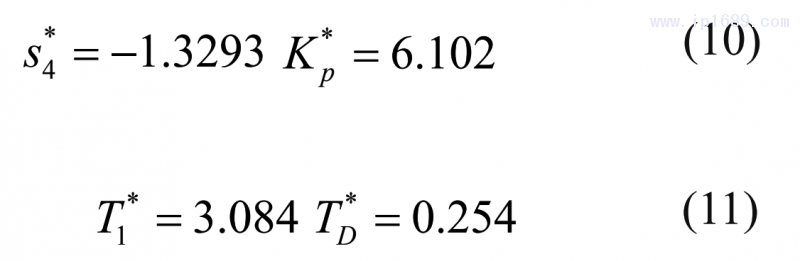
式10-11

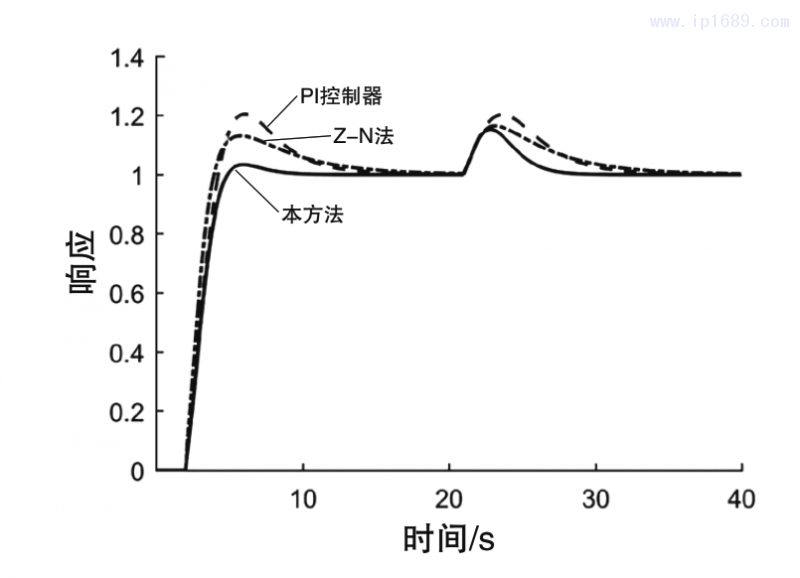
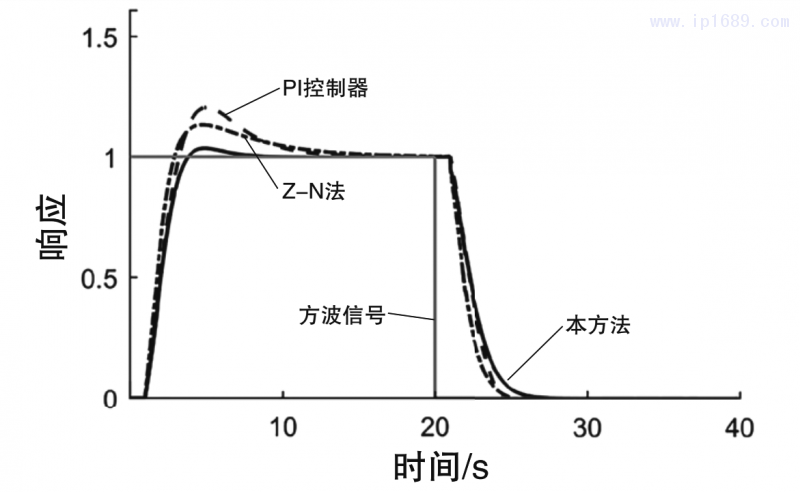
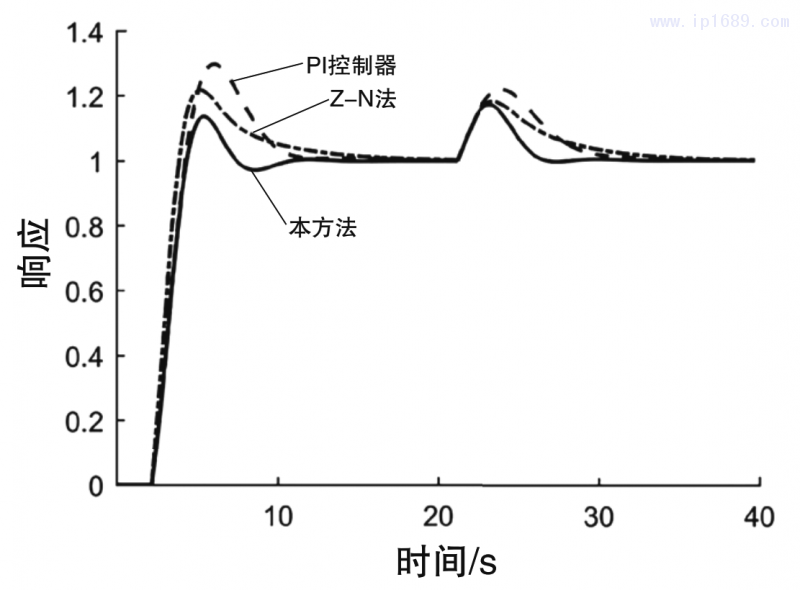
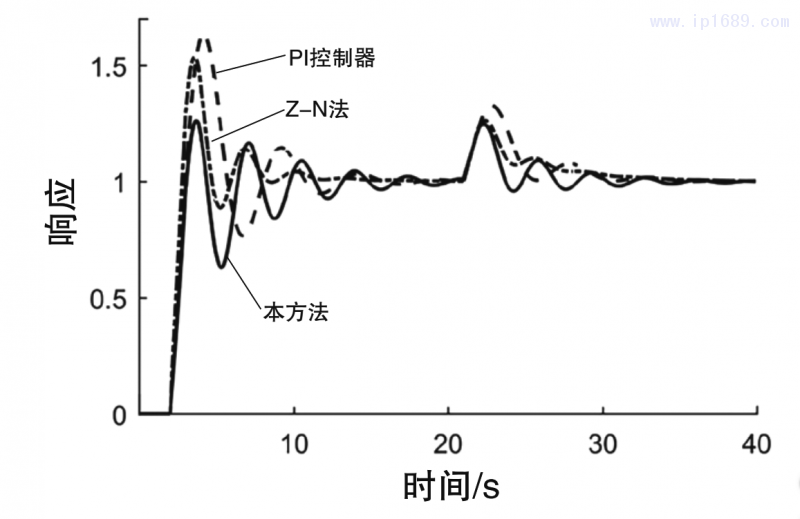
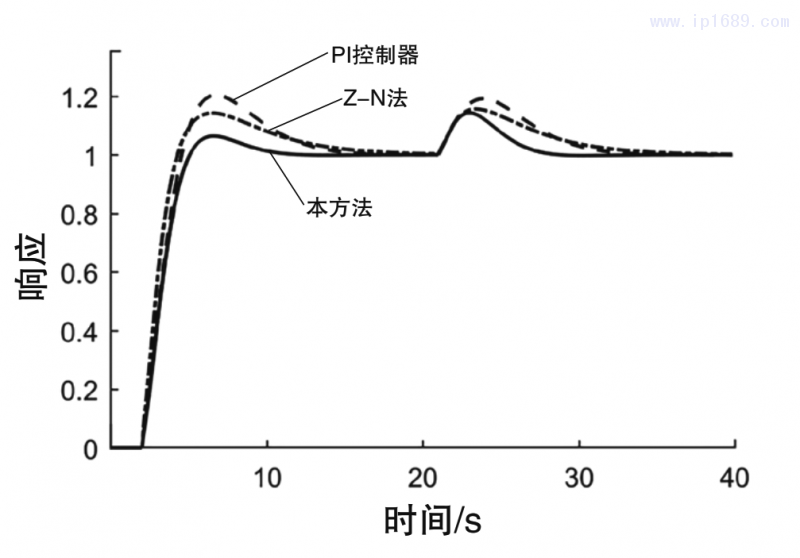
圖2為所有對比方法的伺服響應和調節響應圖；圖3為閉環系統的方波響應圖；圖4為在時間常數k1過程系統模型比例常數由1變為2時的閉環響應曲線圖，即失配情形1；圖5為在時滯參數Td由1變為1.4時的閉環響應曲線圖，即失配情形2；圖6為在時間參數T1由8變為9時的閉環響應曲線圖，即失配情形3。

從圖2可以看出，相比于PI控制器和使用Z-N法的PID控制器，本研究所采用的方法的伺服性能和擾動抑制性能最好，同時具有快速的上升時間和最小的超調量。相反PI控制器所在閉環系統的伺服響應最大的超調量，同時其擾動性能最差。使用Z-N法的PID控制器同樣具有較差的調節性能，其伺服性能比PI控制器的稍微好一些。

由圖3的方波響應圖可以觀察到，本研究所采用的方法在跟隨給定信號的能力方面均優于常規PI控制器和使用Z-N法整定參數的PID控制器。

圖4、圖5和圖6均給過程模型增加不同的攝動，以觀察各種控制器在系統模型失配的情形下響應效果，可以看出即使在系統參數不穩定的情形下，本研究所采用的方法依舊表現出最佳的伺服性能和擾動抑制性能及良好的魯棒性能。

3 結論

本研究探討了塑料薄膜生產中的吹塑機的張力控制系統的魯棒控制，在現有文獻研究的基礎上，提出了一種新的基于MDP方法的PID控制器的設計方法。基于一個假設，即存在一個穩定的實主導極點并且過程控制結構是無振蕩的。同時，需要假設非主導的極點或者零點對控制過程的影響不顯著。為了得到多主極點和PID控制器的可調參數，利用Matlab求解多組特征方程對s的各階導數而組成的聯立方程組。在吹塑機的張力控制系統的一階積分時滯系統下進行了仿真實驗，結果表明，本方法具有良好的追蹤性能和調節性能，并且魯棒性較好，非常適用于張力控制系統的設計。后續研究中將考慮使用優化算法，比如粒子群算法，遺傳算法等結合多主導極點控制方法，使得所得到的控制器性能更加良好，此外將添加更多的優化目標，使得所設計的控制器更加適用于張力控制系統。

參考文獻

[1] 傅明華，汪羞德，顧仲蘭，等. 多功能轉光塑料薄膜應用效應研究[J]. 農業工程學報，2000， 16(6): 81-84.

[2] 竇思紅，謝蘭桂，趙霞，等. 測量塑料薄膜氧氣透過量的不確定度評定[J]. 塑料, 2018(3): 72-75.

[3] 黃身岐，林本農，唐健玲. 可控光、生物降解塑料薄膜工業化生產及應用研究[J]. 福建輕紡，2003(11): 1-9.

[4] 趙海麗，徐婉琪，楊元秀. 塑料薄膜在農業生產中的應用現狀、問題、前景[J]. 南方農業，2014(15): 36-37.

[5] 王欣，王克儉. 農用大棚塑料薄膜材料發展綜述[J]. 塑料包裝， 2019(3): 22-31.

[6] 王盛楠，王亦紅. 基于塑料薄膜疵點檢測的生產設備故障診斷[J]. 機械制造與自動化, 2013， 42(2): 54-56.

[7] 孟新宇. 塑料薄膜壓延過程的計算機仿真系統設計研究[J]. 塑料工業, 2016，44(3): 96-127.

[8] 羅海. 聚乙烯生產工藝技術探討[J]. 綠色環保建材， 2019(8): 31-37.

[9] 姚暢. 塑料瓶新型吹瓶設備結構設計[J]. 內江科技, 2018, 39(1): 44-51.

[10] 劉軍強. 多層中空吹塑機頭的技術進展及創新[J]. 塑料包裝, 2017, 27(5): 15-20.

[11] 杜巧連，陳衛增，俞鴻斌. 吹塑機型坯壁厚控制系統的優化設計[J]. 液壓與氣動， 2005(10): 64-66.

[12] 張航. PLC在全自動吹塑機電氣控制系統中的應用[J]. 廣東石油化工學院學報, 2009，19(6): 33-36.

[13] 黃虹，李子平. 吹塑機自動風環原理及應用[J]. 塑料包裝, 2005(5): 40-41, 35.

[14] 張航，鄧昌奇. 基于PLCN:N網絡的模內貼標吹塑機控制系統設計[J].機床與液壓，2012, 40(14): 101-103.

[15] 王安，李曉娟. BP神經網絡PID控制在吹塑機系統中的應用[J]. 計算機仿真，2010(9): 161-164, 180.

[16] 吳宏鑫，沈少萍. PID控制的應用與理論依據[J]. 控制工程， 2003(1): 39-44.

[17] 景微娜，左信. 幾種PID控制器設計方法的比較[J]. 計算機仿真, 2008，25(1): 270-273.

[18] 陳永慶. 基于Z-N算法的PID爐溫控制[J]. 大連交通大學學報，2008(2): 43-50.

[19] 王冰,方躍法. PID控制器設計的頻域性能圖譜法[J]. 控制工程， 2018， 25(11): 1 953-1 958.

[20] 張曉路，于全訓. 用于不穩定系統的PID調節法[J]. 山東建筑工程學院學報，2000，15(2): 51-55.

[21] 劉紅軍，韓璞，孫海蓉，等. 基于內模控制的PID控制器的設計[J]. 計算機仿真， 2005，22(3): 207-210.

[22] 孫德敏，楊彬彥. 相關系數辨識法PID自動整定軟件及其工業應用[J].中國科學技術大學學報， 1995，25(4): 425-430.

[23] 姜金華，陳永良. 基于PID算法的二自由度自調節測高系統設計[J]. 自動化儀表， 2017，38(12): 17-23.

[24] 楊延西,劉丁. 基于模糊遺傳算法的二自由度PID控制器優化設計[J].儀器儀表學報, 2006(8): 50-54.

[25] 歐林林，張衛東，顧誕英. PID控制作用下一階時滯系統的魯棒穩定性分析[J]. 上海交通大學學報，2006(11): 100-104.

[26] 蔣龍，施衛，王浩，等. 基于遺傳算法優化的無刷電機控制系統設計[J].電子制作，2019(17): 23-26.

[27] 穆海芳,韓君,李明. 改進的粒子群算法在磨煤機PID神經網絡控制中的應用[J]. 金陵科技學院學報, 2019(2): 16-20.

[28] 邱麗，曾貴娥，朱學峰，等.幾種PID控制器參數整定方法的比較研究[J]. 自動化技術與應用，2005(11): 31-34.

[29] 劉喆，李杰，劉俊，等. 改進型Z-N參數整定方法及其硬件實現[J]. 科技通報，2012(2): 109-111.

[30] Arbogast J E, Cooper D J. Extension of IMC tuning correlations for non-self regulating (integrating) processes[J]. ISA Transactions, 2007, 46(3): 303-311.

[31] Begum K G，Rao A S，Radhakrishnan T K. Maximum sensitivity based analytical tuning rules for PID controllers for unstable dead time processes[J]. Chemical Engineering Research and Design, 2016, 109: 593-606.